本文轉(zhuǎn)載自公眾號(hào)“讀芯術(shù)”(ID：AI_Discovery)。

激活函數(shù)是人工神經(jīng)網(wǎng)絡(luò)的驅(qū)動(dòng)因素，其位于神經(jīng)元之上，并管理著神經(jīng)元行為，比如是否需要處理某個(gè)輸入數(shù)據(jù)，若需要，又以何種程度處理等等。從技術(shù)上來(lái)講，某個(gè)節(jié)點(diǎn)的激活函數(shù)將其在神經(jīng)網(wǎng)絡(luò)中前一個(gè)節(jié)點(diǎn)的數(shù)據(jù)輸入，并輸出一個(gè)確定值，這個(gè)值繼而指導(dǎo)后續(xù)節(jié)點(diǎn)如何發(fā)動(dòng)來(lái)響應(yīng)特定輸入信號(hào)。

[[374794]]

本文剖析由激活函數(shù)組成的神經(jīng)網(wǎng)絡(luò)，以及神經(jīng)網(wǎng)絡(luò)的生物類似物，并簡(jiǎn)要介紹幾種常用的激活函數(shù)。

神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)

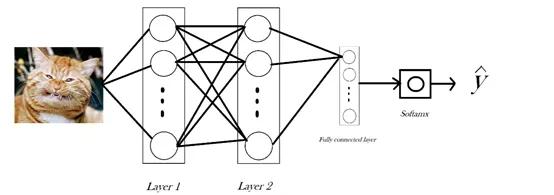
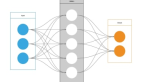
作為一名數(shù)據(jù)科學(xué)愛(ài)好者，你一定見(jiàn)過(guò)上面的這張圖片或者與之相似的圖片。這張圖片是對(duì)雙層神經(jīng)網(wǎng)絡(luò)工作流程的經(jīng)典描述。如圖，該網(wǎng)絡(luò)對(duì)貓或狗的圖片進(jìn)行分類，其中有兩個(gè)隱藏層，每一層包含一行神經(jīng)元，一行有16個(gè)。我們把圖片局部放大，放大第二層的第一個(gè)神經(jīng)元。

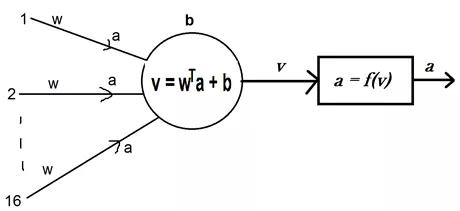
局部放大之后大致如此。注意，此神經(jīng)元接受前16個(gè)神經(jīng)元傳遞的信號(hào)。神經(jīng)元將連接權(quán)值與信號(hào)相乘，并在乘積上加上一個(gè)偏差項(xiàng)，最后得到計(jì)算結(jié)果，并將其命名為v。此v可視為這個(gè)神經(jīng)元對(duì)所輸入圖像的認(rèn)知。

在識(shí)別到輸入信號(hào)之后，神經(jīng)元可產(chǎn)生相應(yīng)的反應(yīng)，在此激活函數(shù)發(fā)揮其作用。激活函數(shù)被命名為f()，作為由識(shí)別到反應(yīng)的映射，產(chǎn)生值a，并將其傳遞到下一層神經(jīng)元，作為前一層特定神經(jīng)元對(duì)信號(hào)做出反應(yīng)的標(biāo)志。

生物學(xué)類比

假如將手放在逐漸升溫的鋼鍋上，一旦溫度超過(guò)某個(gè)閾值，你就會(huì)急切地要拿開(kāi)手。把手移開(kāi)時(shí)并不需要知道鍋的確切溫度，而是根據(jù)實(shí)際參數(shù)做出選擇。這是神經(jīng)元在放電，當(dāng)神經(jīng)元放電時(shí)，指令傳遞到外圍(本例中的手)。

這就是激活函數(shù)的來(lái)源或者至少與之相似。在這里實(shí)際數(shù)據(jù)是冗余的，神經(jīng)元只需判斷其是否超過(guò)閾值。

就目前所知，生物神經(jīng)元和人工神經(jīng)元之間的一個(gè)顯著差異是，前者要么被激活，要么不被激活，只有兩種結(jié)果，而后者的激活程度是在一定范圍內(nèi)。

激活函數(shù)的種類

激活函數(shù)多種多樣。讓我們按照函數(shù)所解決問(wèn)題的順序，大致學(xué)習(xí)其中的幾種：

問(wèn)題1：學(xué)習(xí)問(wèn)題

早期，神經(jīng)網(wǎng)絡(luò)的目標(biāo)是學(xué)習(xí)自身，線性函數(shù)的處理效果相當(dāng)好。之所以稱為線性函數(shù)，是因?yàn)関 = wa + b的近似值與直線方程y = mx + c極為相似。

問(wèn)題2：非線性問(wèn)題

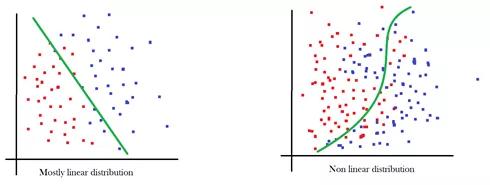
雖然線性函數(shù)非常接近于右側(cè)數(shù)據(jù)，但是左側(cè)數(shù)據(jù)卻效果不佳。由于非線性分布數(shù)據(jù)集主導(dǎo)著機(jī)器學(xué)習(xí)領(lǐng)域，而且激活函數(shù)是將非線性注入到網(wǎng)絡(luò)中的唯一適用方法，所以函數(shù)就不能是線性的。能夠解決這個(gè)問(wèn)題的常見(jiàn)函數(shù)有：

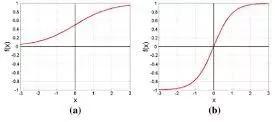
Sigmoid函數(shù)：在函數(shù)內(nèi)輸入一個(gè)值，輸出值的范圍為(0,1)。輸入的值越小，輸出值越接近于0，輸入的值越大，輸出值則越接近于1，但都不會(huì)達(dá)到任一個(gè)極限值。

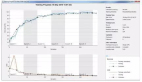
tanh函數(shù)：也稱雙曲正切函數(shù)。tanh函數(shù)與sigmoid函數(shù)非常相似，只是輸出值范圍為(-1，1)。右側(cè)為sigmoid函數(shù)圖像，左側(cè)為tanh函數(shù)圖像。

問(wèn)題3：梯度消失問(wèn)題

再次觀察圖表，sigmoid函數(shù)曲線越接近于極限值越平緩，也就是說(shuō)，當(dāng)輸入絕對(duì)值非常大的值的時(shí)候，輸出值的變化不明顯。這大大降低了學(xué)習(xí)率。這就是所謂的梯度消失問(wèn)題，隨著進(jìn)程推進(jìn)，梯度(比如，學(xué)習(xí))消失。ReLU函數(shù)解決了這個(gè)問(wèn)題，實(shí)際上它也是現(xiàn)代神經(jīng)網(wǎng)絡(luò)的默認(rèn)激活函數(shù)。

ReLU函數(shù)：ReLU函數(shù)是線性整流函數(shù)(Rectified Linear Unit)的簡(jiǎn)稱，它可能是最有趣、最反直覺(jué)的函數(shù)。它幾乎就是一個(gè)直線函數(shù)，只不過(guò)在原點(diǎn)處有個(gè)拐角，所以它是一個(gè)分段函數(shù)。

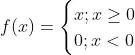
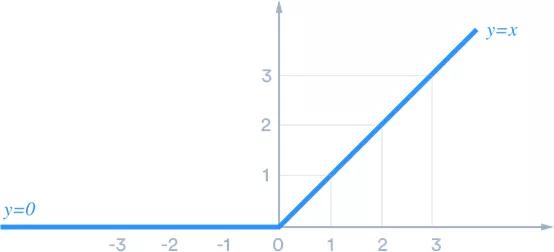
人們經(jīng)常會(huì)問(wèn)，一個(gè)近似線性的函數(shù)是如何解決這個(gè)問(wèn)題的。從圖中可以明顯看出，它幾乎可以完全避免梯度消失問(wèn)題。單個(gè)ReLU函數(shù)會(huì)顯得比較單調(diào)乏味，但是多個(gè)在一些就會(huì)變得無(wú)懈可擊。

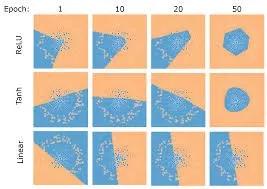
線性函數(shù)完全無(wú)法近似，而tanh函數(shù)試圖畫(huà)出平滑的類圓曲線，所以最終出現(xiàn)了六角形邊狀的ReLU函數(shù)。你可能會(huì)認(rèn)為，這是兩個(gè)直線的一端接在一起，如同鐘表指針那樣。

現(xiàn)在，假設(shè)有一百萬(wàn)條這樣的直線，那么你可以用這種排列方法模擬任何非線性形狀。ReLU的精妙之處就在于，它既近似線性，多個(gè)組在一起時(shí)又能通過(guò)改變拐角的角度模擬出幾乎所有形狀。

這引出了最后一個(gè)要解決的問(wèn)題。

問(wèn)題4：概率和問(wèn)題

無(wú)論隱藏層的工作內(nèi)容如何，最終的目標(biāo)都是生成某種預(yù)測(cè)，而在這里，就是輸出一個(gè)概率向量，其中包含輸入對(duì)象為已標(biāo)記對(duì)象概率表。比如，第一張圖片中神經(jīng)網(wǎng)絡(luò)的結(jié)果可能是：

[dog, cow, cat, goat, lamb] = [0. 2, 0.05, 0.7,0.03, 0.01] 

結(jié)果最有可能是貓，因?yàn)槭秦埖母怕蕿?.7，概率最高。

為了將全連接層的最終輸出值轉(zhuǎn)換為正規(guī)化概率向量，需要一個(gè)函數(shù)接受一個(gè)向量，然后輸出另一個(gè)向量，而且輸出向量所有元素的和為1。畢竟，這才是概率向量。

Sigmoid函數(shù)非常接近于概率函數(shù)，因?yàn)樗妮敵鲋捣秶鸀?到1，但是不滿足和等于1的情況。Softmax函數(shù)可以滿足這一點(diǎn)。

Softmax函數(shù)：函數(shù)接受一個(gè)向量，并使用下列函數(shù)計(jì)算輸出向量中每個(gè)元素的相應(yīng)概率。

函數(shù)中分母為所有可能分子的和，避免輸出值超過(guò)1。

關(guān)于激活函數(shù)，你了解了嘛?