回溯算法-機(jī)器人的運(yùn)動(dòng)范圍
本文轉(zhuǎn)載自微信公眾號(hào)「神奇的程序員K」,作者神奇的程序員K。轉(zhuǎn)載本文請(qǐng)聯(lián)系神奇的程序員K公眾號(hào)。
前言
有一個(gè)矩陣,機(jī)器人可以從坐標(biāo)(0,0)的格子開始移動(dòng),它每次可以向左、右、上、下移動(dòng)一格,但是不能進(jìn)入行坐標(biāo)和列坐標(biāo)的數(shù)位之和大于K的格子,求這個(gè)機(jī)器人總共能走多少個(gè)格子以及它的行動(dòng)軌跡。
本文就跟大家分享下這個(gè)問題的解決方案 ,歡迎各位感興趣的開發(fā)者閱讀本文。
實(shí)現(xiàn)思路
在上一篇講解尋找矩陣中的路徑文章中,我們學(xué)會(huì)了使用回溯算法來訪問矩陣中的格子,本文要討論的這個(gè)問題在訪問格子之前做了一層判斷,如果滿足條件就能進(jìn)入,不滿足就無法進(jìn)入。
我們要做的這層判斷為:計(jì)算出待訪問格子的坐標(biāo)的數(shù)位之和,如果其大于K(最大活動(dòng)范圍)則不能訪問。
數(shù)位之和:即取出數(shù)字中每個(gè)位置的值,將其相加得出的結(jié)果。例如:19的數(shù)位之和就是1 + 9 = 10。
判斷當(dāng)前格子是否已訪問
首先,我們需要?jiǎng)?chuàng)建一個(gè)與原矩陣大小相同的矩陣,用于標(biāo)識(shí)機(jī)器人是否已走這個(gè)格子。
在js中無法直接創(chuàng)建指定大小的二維數(shù)組,創(chuàng)建思路如下:
- 以矩陣的長(zhǎng)度為大小創(chuàng)建一個(gè)數(shù)組
- 遍歷創(chuàng)建好的數(shù)組,再以矩陣的第0號(hào)數(shù)組的長(zhǎng)度為大小創(chuàng)建數(shù)組,賦值給遍歷到的每一項(xiàng)。
判斷格子是否可進(jìn)入
在訪問格子時(shí),我們需要判斷下要訪問的格子是否能進(jìn)入,我們需要計(jì)算出行坐標(biāo)與列坐標(biāo)的數(shù)位之和,然后將其相加,判斷相加后的結(jié)果是否大于機(jī)器人的最大活動(dòng)范圍(K)。
計(jì)算數(shù)位之和有兩種做法:
- 將數(shù)字轉(zhuǎn)為字符串,遍歷取出每個(gè)字符將其轉(zhuǎn)為數(shù)字后再相加
- 對(duì)數(shù)字進(jìn)行模運(yùn)算,將其結(jié)果相加,再對(duì)數(shù)字本身進(jìn)行/10操作,直至數(shù)字小于等于0
開始移動(dòng)機(jī)器人
移動(dòng)機(jī)器人時(shí),我們需要7個(gè)參數(shù):
- 矩陣的總行數(shù)
- 矩陣的總列數(shù)
- 即將進(jìn)入格子的行坐標(biāo)
- 即將進(jìn)入格子的列坐標(biāo)
- 最大活動(dòng)范圍
- 訪問標(biāo)識(shí)矩陣
- 路徑矩陣
首先,我們需要進(jìn)行邊界條件判斷(遞歸的終止條件),條件滿足代表該格子無法訪問,可行走格子為0(直接返回0):
- 待訪問格子的行坐標(biāo)大于矩陣的總行數(shù)
- 待訪問格子的行坐標(biāo)小于0
- 待訪問格子的列坐標(biāo)大于矩陣的總列數(shù)
- 待訪問格子的列坐標(biāo)小于0
- 當(dāng)前格子已經(jīng)被訪問
- 當(dāng)前格子不能進(jìn)入
如果上述條件都滿足則表示當(dāng)前格子可以訪問,保存當(dāng)前格子中的值到行動(dòng)軌跡中,標(biāo)識(shí)當(dāng)前格子為已訪問狀態(tài),已行走格子數(shù)+1,并遞歸嘗試當(dāng)前格子的其它四個(gè)方向的格子能否進(jìn)入。
當(dāng)遞歸棧清空后,我們也就得到了機(jī)器人總共可以進(jìn)入的格子總數(shù)以及它的行動(dòng)軌跡。
實(shí)現(xiàn)代碼
接下來,我們將上述思路轉(zhuǎn)換為TypeScript代碼。
格子能否進(jìn)入函數(shù)
我們先來看下判斷當(dāng)前格子能否進(jìn)入的函數(shù)實(shí)現(xiàn),如下所示:
- /**
- * 判斷機(jī)器人能否進(jìn)入目標(biāo)格子
- * @param row 行坐標(biāo)
- * @param col 列坐標(biāo)
- * @param target 臨界點(diǎn)
- * @private
- */
- private checkPath(row: number, col: number, target: number): boolean {
- // 兩坐標(biāo)的數(shù)位之和必須小于等于臨界點(diǎn)
- return sumOfDigits(row) + sumOfDigits(col) <= target;
- }
- // 轉(zhuǎn)字符串實(shí)現(xiàn)
- export function sumOfDigits(target: number): number {
- let finalVal = 0;
- const computeVal = target.toString();
- for (let i = 0; i < computeVal.length; i++) {
- finalVal += Number(computeVal[i]);
- }
- return finalVal;
- }
- // 數(shù)位之和 - 模運(yùn)算實(shí)現(xiàn)
- export function sumOfDigitsForModular(target: number): number {
- let finalVal = 0;
- while (target > 0) {
- finalVal += Math.floor(target % 10);
- target /= 10;
- }
- return finalVal;
- }
移動(dòng)機(jī)器人函數(shù)
移動(dòng)機(jī)器人至指定格子實(shí)現(xiàn)代碼如下所示:
- /**
- * 開始移動(dòng)機(jī)器人
- * @param rows 矩陣總行數(shù)
- * @param cols 矩陣總列數(shù)
- * @param row 待進(jìn)入格子的行坐標(biāo)
- * @param col 待進(jìn)入格子的列坐標(biāo)
- * @param threshold 最大活動(dòng)范圍
- * @param isVisited 訪問標(biāo)識(shí)矩陣
- * @param matrix 路徑矩陣
- * @private
- */
- rivate startMoving(
- rows: number,
- cols: number,
- row: number,
- col: number,
- threshold: number,
- isVisited: Array<Array<boolean>>,
- matrix: Array<Array<T>>
- ): number {
- // 邊界條件判斷
- if (
- row >= rows ||
- row < 0 ||
- col >= cols ||
- col < 0 ||
- isVisited[row][col] ||
- !this.checkPath(row, col, threshold)
- ) {
- return 0;
- }
- // 記錄當(dāng)前訪問的格子內(nèi)容
- this.path += `${matrix[row][col]} -> `;
- // 標(biāo)識(shí)當(dāng)前格子已被訪問
- isVisited[row][col] = true;
- // 格子訪問數(shù)量+1
- return (
- 1 +
- this.startMoving(rows, cols, row + 1, col, threshold, isVisited, matrix) +
- this.startMoving(rows, cols, row, col + 1, threshold, isVisited, matrix) +
- this.startMoving(rows, cols, row - 1, col, threshold, isVisited, matrix) +
- this.startMoving(rows, cols, row, col - 1, threshold, isVisited, matrix)
- );
- }
主函數(shù)
最后,我們來看下主函數(shù)的實(shí)現(xiàn),如下所示:
- /**
- * 題目:
- * 地上有一個(gè)m行n列的方格。
- * 一個(gè)機(jī)器人從坐標(biāo)(0,0)的格子開始移動(dòng),
- * 它每次可以向左、右、上、下移動(dòng)一格,但不能進(jìn)入行坐標(biāo)和列坐標(biāo)的數(shù)位之和大于k的格子。
- * 例如,當(dāng)k為18時(shí),機(jī)器人能夠進(jìn)入方格 (35,37),因?yàn)?+5+3+7=18。
- * 但它不能進(jìn)入方格(35,38),因?yàn)?+5+3+8=19. 請(qǐng)問該機(jī)器人能夠到達(dá)多少個(gè)格子?
- * @param matrix 矩陣
- * @param threshold 臨界點(diǎn)(最大活動(dòng)范圍)
- */
- public movingCount(matrix: Array<Array<T>>, threshold = 0): number {
- if (threshold < 0 || matrix.length <= 0) {
- return 0;
- }
- // 獲取方格的總行數(shù)與總列數(shù)
- const rows = matrix.length;
- const cols = matrix[0].length;
- // 創(chuàng)建標(biāo)記數(shù)組,用于標(biāo)識(shí)格子是否被訪問
- const isVisited: Array<Array<boolean>> = new Array(rows);
- for (let i = 0; i < isVisited.length; i++) {
- isVisited[i] = new Array(cols);
- }
- // 從0,0位置開始移動(dòng),計(jì)算總的移動(dòng)格子數(shù)量
- return this.startMoving(rows, cols, 0, 0, threshold, isVisited, matrix);
- }
完整代碼請(qǐng)移步:Backtracking.ts#L80
編寫測(cè)試用例
接下來,我們構(gòu)造一個(gè)矩陣來驗(yàn)證下上述代碼能否正確執(zhí)行,如下所示:
- const pathArr = [
- ["a", "b", "t", "g"],
- ["c", "f", "c", "s"],
- ["j", "d", "e", "h"]
- ];
- const backtracking = new Backtracking<string>();
- const totalCount = backtracking.movingCount(pathArr, 4);
- const path = backtracking.path;
- console.log(
- "機(jī)器人總共可走的格子總數(shù)為: ",
- totalCount,
- ",運(yùn)動(dòng)軌跡為: ",
- path.substr(0, path.length - 3)
- );
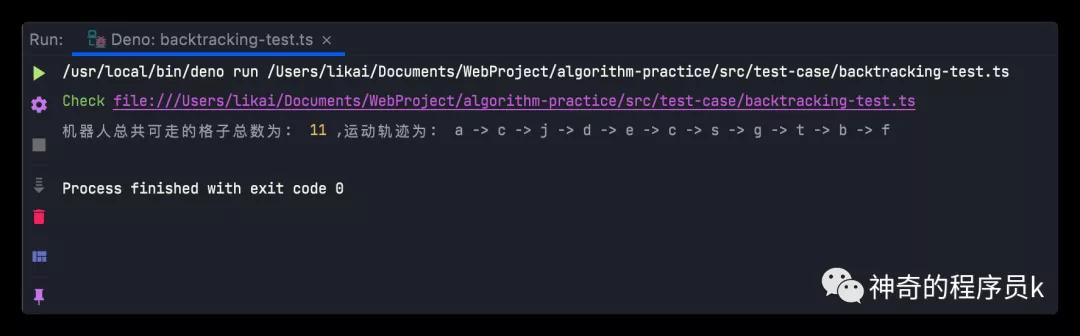
執(zhí)行結(jié)果如下所示: