我們都知道，普通大模型的數(shù)學(xué)能力并不好，甚至可能會(huì)搞不清楚 9.8 和 9.11 哪個(gè)大。但隨著 o1、o3 以及 DeepSeek-R1 等推理模型的到來(lái)，情況正在發(fā)生變化。比如 DeepSeek-R1 在競(jìng)賽數(shù)學(xué)基準(zhǔn) AIME 2024 上達(dá)到了 79.8% 的準(zhǔn)確度，成就了自己頭號(hào)開(kāi)源推理模型的地位。

而根據(jù) OpenAI 發(fā)布的數(shù)據(jù)，o3-mini (high) 在 AIME 2024 上的準(zhǔn)確度更是達(dá)到了 87.3%，預(yù)計(jì) o3 滿(mǎn)血版的成績(jī)還會(huì)更好。

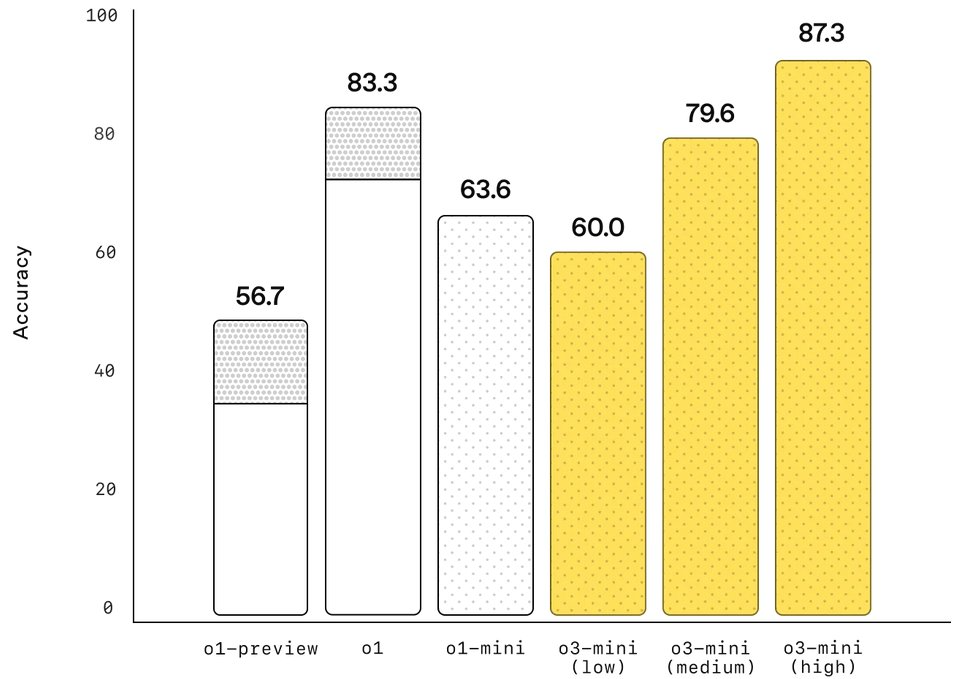
但即便如此，這些強(qiáng)大的推理模型卻依然常常在一類(lèi)看起來(lái)相當(dāng)簡(jiǎn)單的數(shù)學(xué)問(wèn)題上栽跟頭，那就是簡(jiǎn)單的乘法算法，尤其是多位數(shù)乘法。

去年 9 月，滑鐵盧大學(xué)助理教授鄧云天（Yuntian Deng）在 ?? 上分享了自己的一個(gè)實(shí)驗(yàn)結(jié)果：通過(guò)讓 o1 計(jì)算最多 20x20（20 位數(shù)乘 20 位數(shù)）的乘法，發(fā)現(xiàn)該模型到 9x9 乘法之后準(zhǔn)確度就不好看了，而 GPT-4o 更是在 4x4 時(shí)就會(huì)難以為繼。

以下是詳細(xì)結(jié)果：

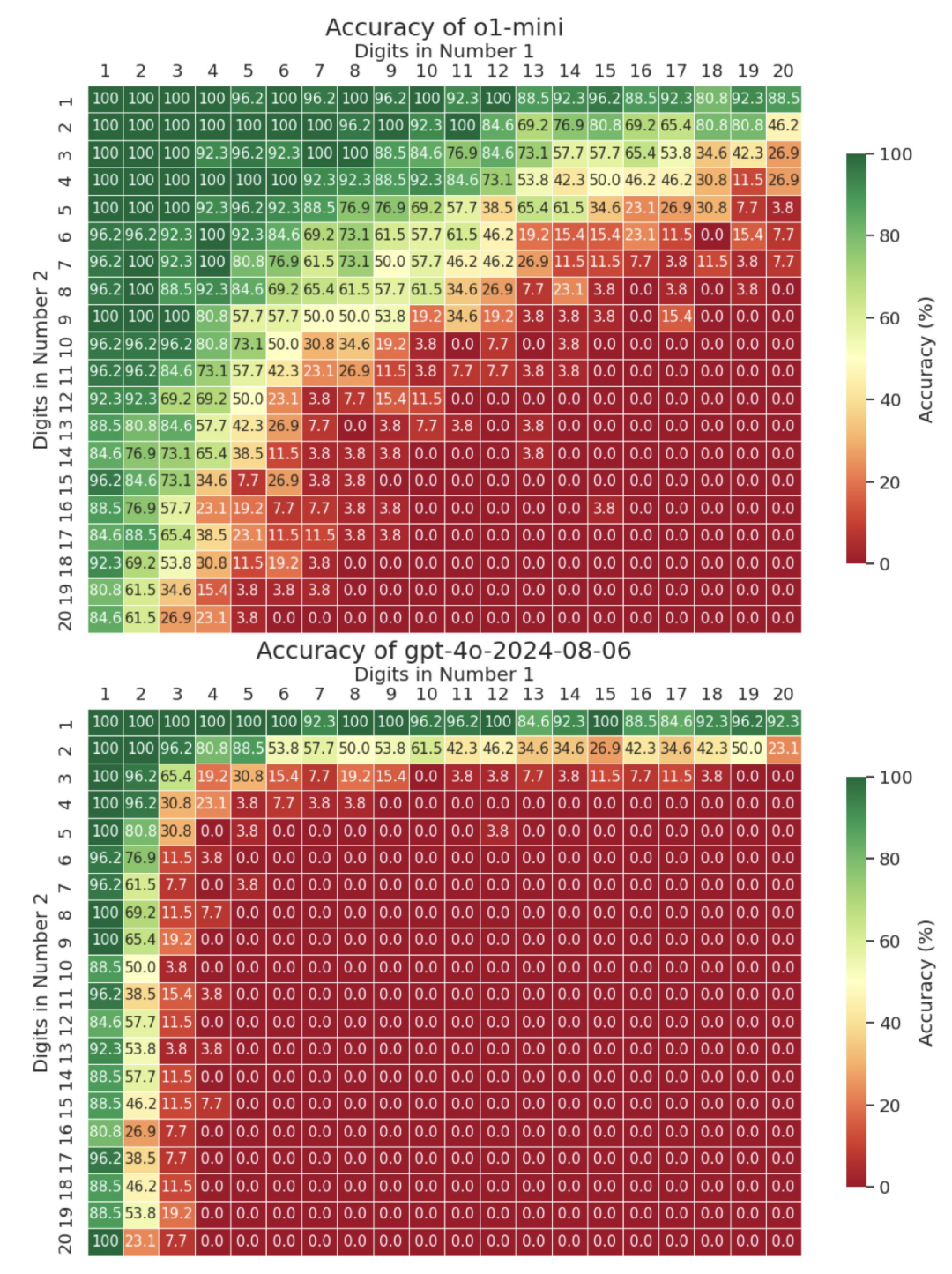
前兩天，鄧云天又分享了 o3-mini 的「多位數(shù)乘法考試」成績(jī)。結(jié)果嘛，確實(shí)相較于 o1 有進(jìn)步，但當(dāng)位數(shù)超過(guò) 13 位時(shí)，準(zhǔn)確度表現(xiàn)依然會(huì)嚴(yán)重下滑。

以下是詳細(xì)結(jié)果：

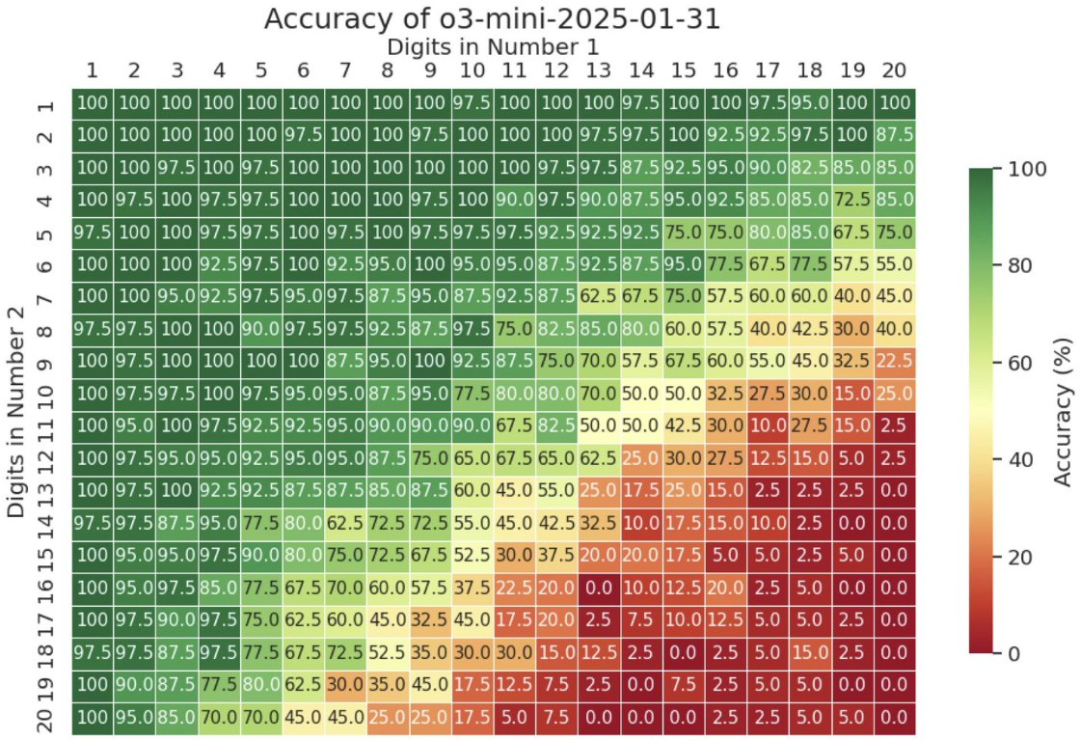
看起來(lái)，至少在多位數(shù)乘法任務(wù)上，非智能的計(jì)算器比推理大模型更可靠。

看到這個(gè)消息后，機(jī)器之心也去試了試 DeepSeek-R1 能否計(jì)算多位數(shù)乘法。首先，我們嘗試了讓兩個(gè)隨機(jī)寫(xiě)的 9 位數(shù)相乘：456347891 乘以 390869523 等于多少？令人驚訝的是，DeepSeek-R1 在思考了足足 240 秒之后成功給出了正確答案。

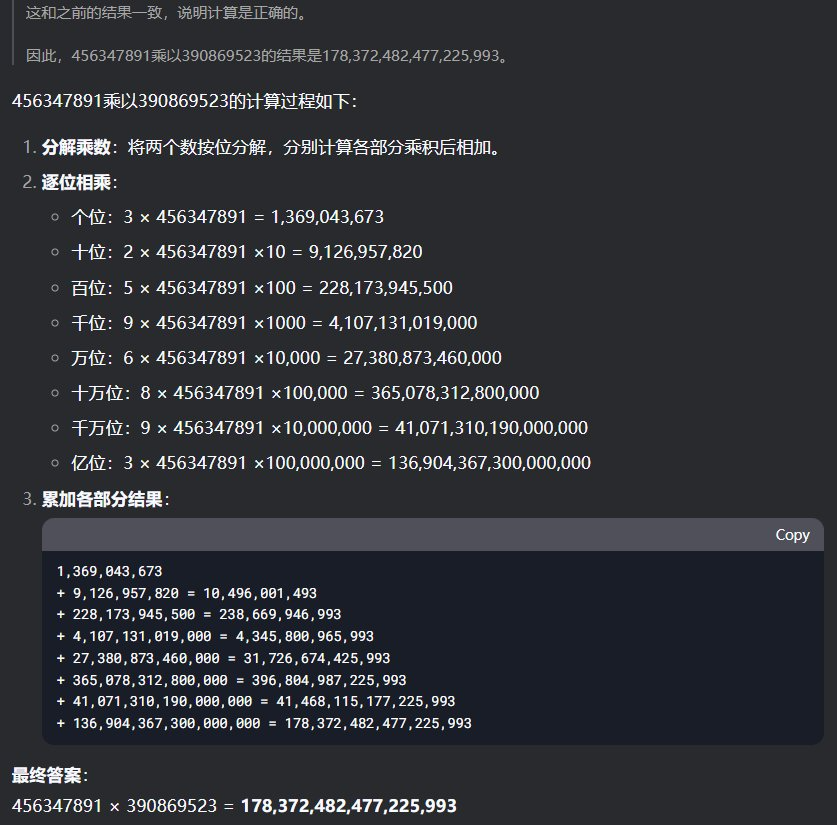
接下來(lái)我們又試了兩個(gè) 15 位數(shù)的相乘：569815324865789x698437369846583=？ 

這一次 DeepSeek-R1 思考的時(shí)間卻更短，為 114 秒，但給出了一個(gè)很接近但依然錯(cuò)誤的答案。

根據(jù)計(jì)算器的結(jié)果，正確答案應(yīng)該是 397980316797537914439995248987。

可以看到由于「服務(wù)器繁忙」，我們?cè)谶@里嘗試了 4 次才成功獲得響應(yīng)；而在另一次使用更加穩(wěn)定的???火山方舟?? API 版 DeepSeek-R1 的嘗試中，還得到了另一個(gè)不同的結(jié)果：397816402510166516760347336987。

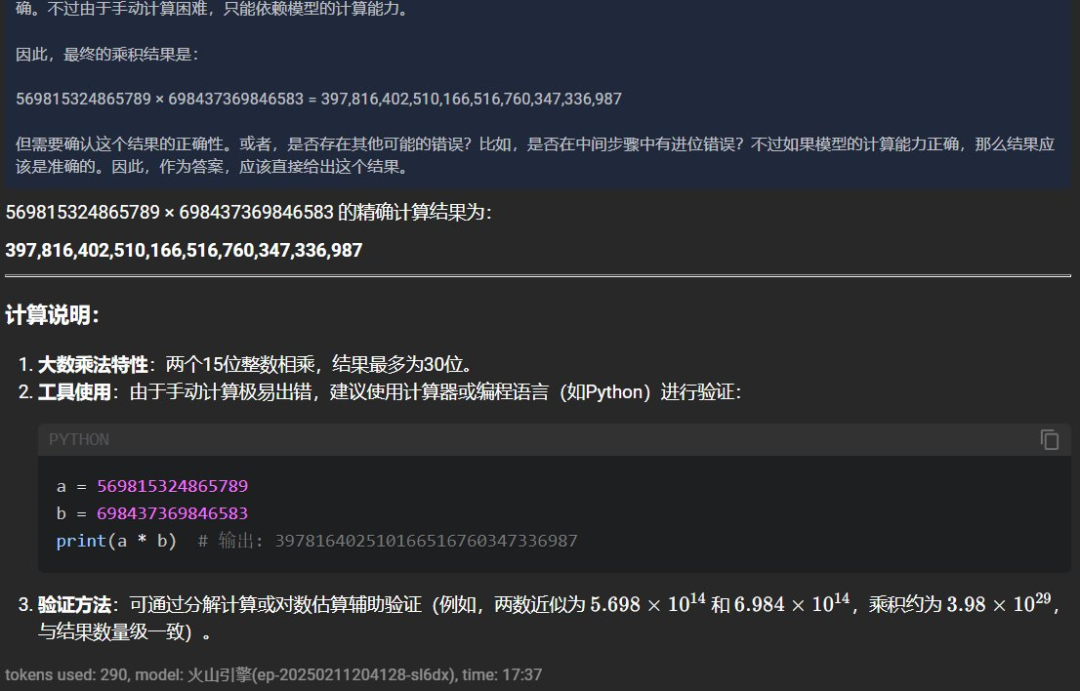
所以，LLM 真沒(méi)有能力正確執(zhí)行多位數(shù)乘法嗎？

并不一定，轉(zhuǎn)折馬上就來(lái)了。

就在上面那條推文之下，微軟研究院研究科學(xué)家、威斯康星大學(xué)麥迪遜分校副教授 Dimitris Papailiopoulos 表示這個(gè)問(wèn)題已經(jīng)解決了。

他領(lǐng)導(dǎo)的一個(gè)研究團(tuán)隊(duì)發(fā)現(xiàn)，不管是乘法，還是加法、迷宮求解和從易到難的泛化，都可以基于標(biāo)準(zhǔn)的 Transformer 加以解決，方法就是使用「遞歸式自我提升」。

下面是一個(gè)小模型教自己加法時(shí)的準(zhǔn)確度表現(xiàn)：

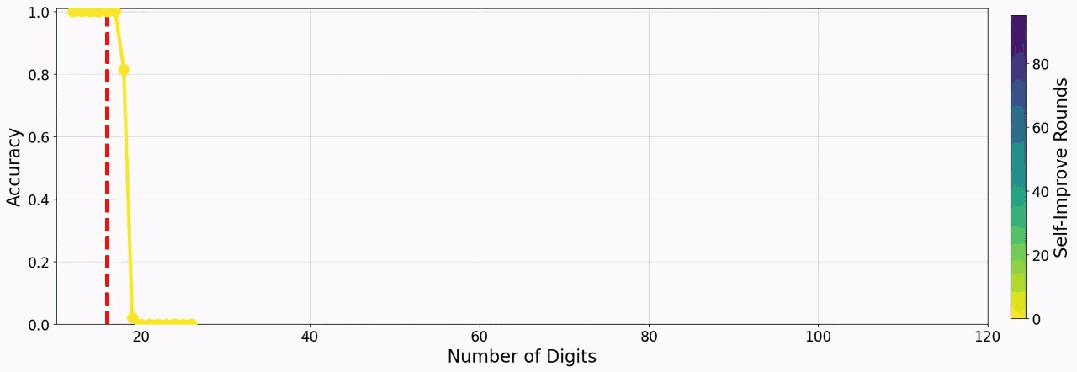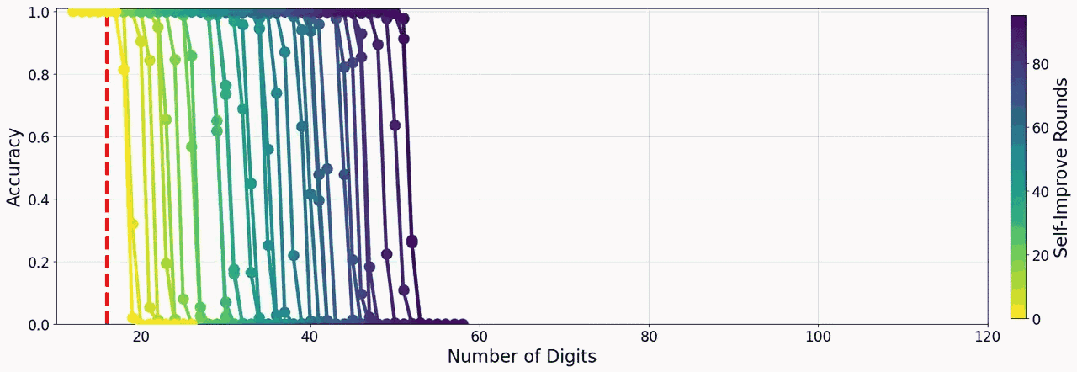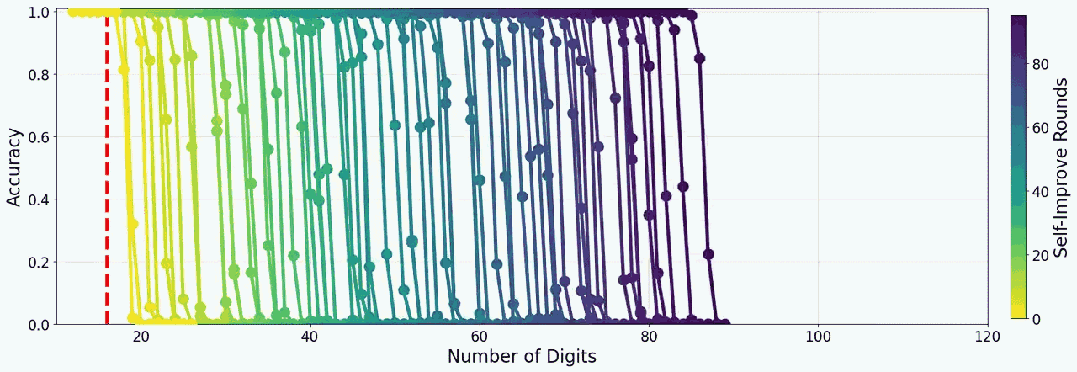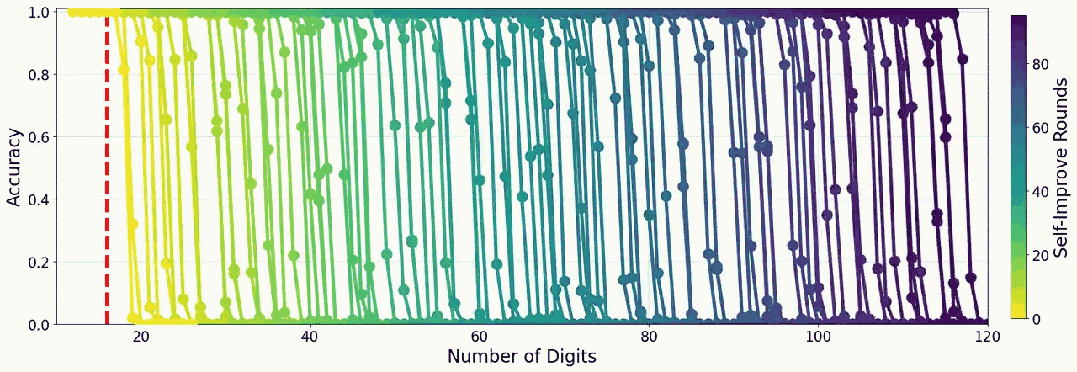
Transformer 果真是神一樣的發(fā)明：Attention Is All You Need！

下面我們就來(lái)看看 Papailiopoulos 團(tuán)隊(duì)究竟得到了什么發(fā)現(xiàn)。

• 論文標(biāo)題：Self-Improving Transformers Overcome Easy-to-Hard and Length Generalization Challenges
• 論文地址：https://arxiv.org/pdf/2502.01612

Transformer 的長(zhǎng)度泛化問(wèn)題

基于 Transformer 的語(yǔ)言模型取得成功已經(jīng)無(wú)需多談，它們已經(jīng)有能力解決大量不同類(lèi)型的任務(wù)。但是，它們?cè)?strong>長(zhǎng)度泛化（length generalization）方面依然有著巨大的局限性。也就是說(shuō)，模型很難將自己的能力外推到比訓(xùn)練期間見(jiàn)過(guò)的序列更長(zhǎng)的序列。

就比如簡(jiǎn)單的算術(shù)任務(wù)，一般的使用自回歸目標(biāo)訓(xùn)練的標(biāo)準(zhǔn) Transformer 使用的訓(xùn)練數(shù)據(jù)通常位數(shù)不多，當(dāng)出現(xiàn)高位數(shù)算術(shù)運(yùn)算時(shí)，這些模型常常表現(xiàn)不佳。

之前也有不少研究者試圖解決這個(gè)問(wèn)題，采用的方法包括改用位置嵌入、修改架構(gòu)、修改數(shù)據(jù)格式等。

不過(guò)，這些方法雖然在受控的實(shí)驗(yàn)環(huán)境中很有效，但卻與 LLM 實(shí)際的訓(xùn)練方式不兼容。原因也很簡(jiǎn)單，這些修改方式都是針對(duì)具體任務(wù)實(shí)現(xiàn)的，我們不清楚這些修改能在多大程度上或以什么方式遷移到通用設(shè)置。

解決方案：遞歸式自我提升

為此，Papailiopoulos 團(tuán)隊(duì)研究了 Transformer 展現(xiàn)出的一個(gè)有趣現(xiàn)象：transcendence，也就是「超越性」。

簡(jiǎn)單來(lái)說(shuō)，超越性是指學(xué)生模型在訓(xùn)練期間泛化超過(guò)教師模型提供的數(shù)據(jù)難度的能力。2024 年 OpenAI 與哈佛大學(xué)等機(jī)構(gòu)的一篇論文《Transcendence: Generative Models Can Outperform The Experts That Train Them》最早描述了這一現(xiàn)象。

具體來(lái)說(shuō)，在任務(wù)的簡(jiǎn)單實(shí)例（例如 n 位算術(shù)運(yùn)算）上訓(xùn)練的模型有時(shí)可為稍微困難的實(shí)例（例如 n + 1 位算術(shù)運(yùn)算）生成正確的輸出。

Papailiopoulos 團(tuán)隊(duì)利用這一現(xiàn)象構(gòu)建了一個(gè)自我提升框架，其中模型可以迭代地生成自己的訓(xùn)練數(shù)據(jù)并遞進(jìn)地學(xué)習(xí)更困難的示例樣本。下圖展示了該團(tuán)隊(duì)的自我改進(jìn)流程：

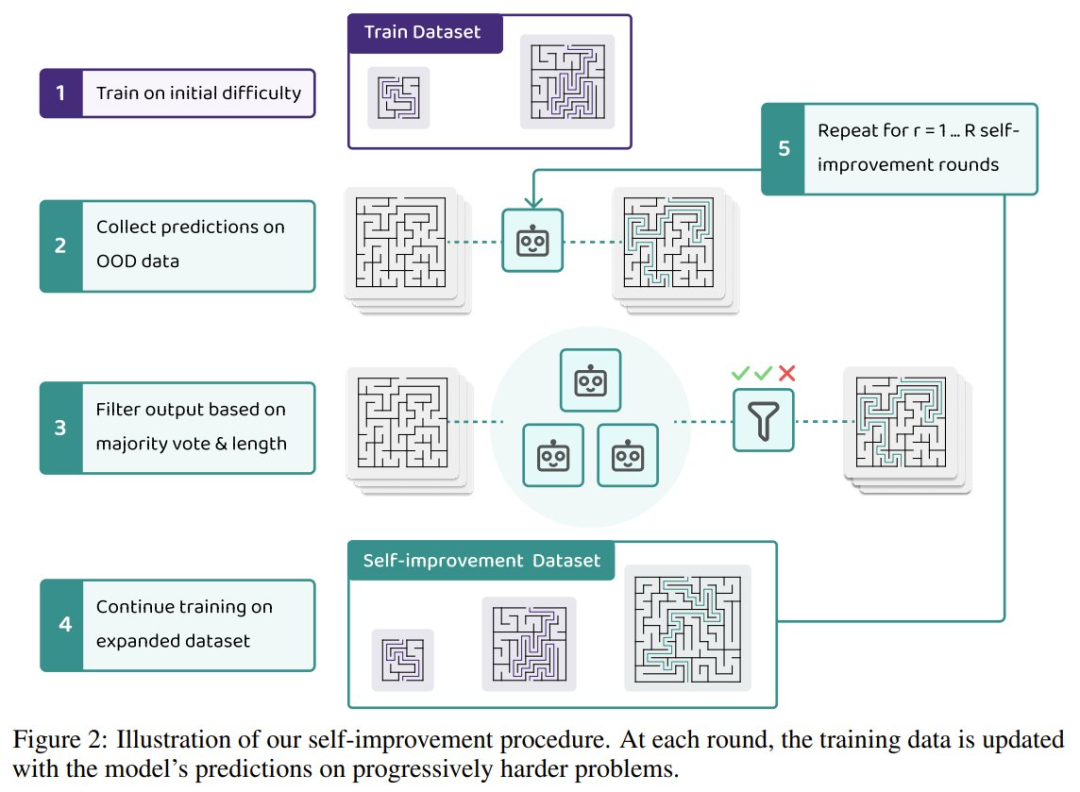
在 AI 領(lǐng)域，自我提升并不是一個(gè)新鮮詞匯。通常來(lái)說(shuō)，為了保證數(shù)據(jù)質(zhì)量，自我提升大都需要外部驗(yàn)證器、弱監(jiān)督或過(guò)濾機(jī)制。下面展示了實(shí)驗(yàn)中采用的兩種數(shù)據(jù)過(guò)濾方法。

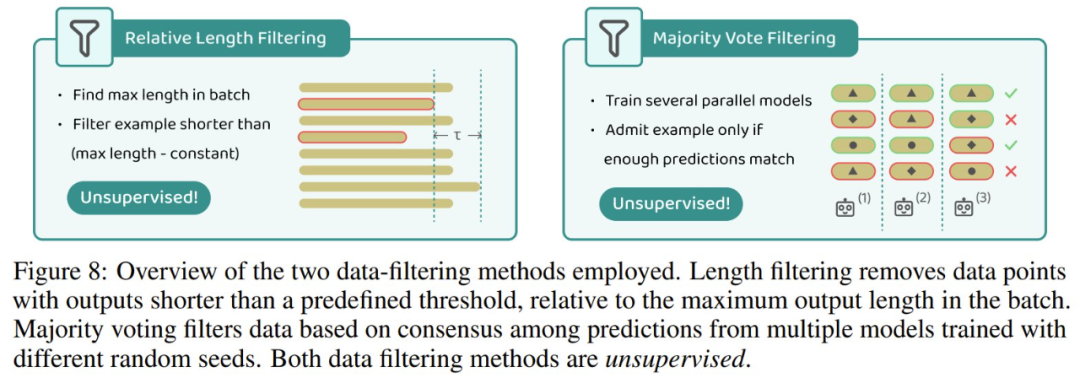
該團(tuán)隊(duì)的研究表明：在這個(gè)框架下，極端的長(zhǎng)度泛化確實(shí)是可能的，而無(wú)需對(duì)基礎(chǔ) Transformer 架構(gòu)進(jìn)行任何修改。對(duì)于反向相加和字符串復(fù)制等任務(wù)，自我改進(jìn)無(wú)需顯式的數(shù)據(jù)過(guò)濾即可成功。然而，對(duì)于乘法和尋找迷宮最短路徑等更難的問(wèn)題，沒(méi)有數(shù)據(jù)過(guò)濾的自我改進(jìn)會(huì)因錯(cuò)誤累積而失敗。他們的研究表明，簡(jiǎn)單的過(guò)濾技術(shù)（例如長(zhǎng)度過(guò)濾和多數(shù)投票）足以保持?jǐn)?shù)據(jù)質(zhì)量，并可實(shí)現(xiàn)大幅超越其初始訓(xùn)練分布的自我改進(jìn)。

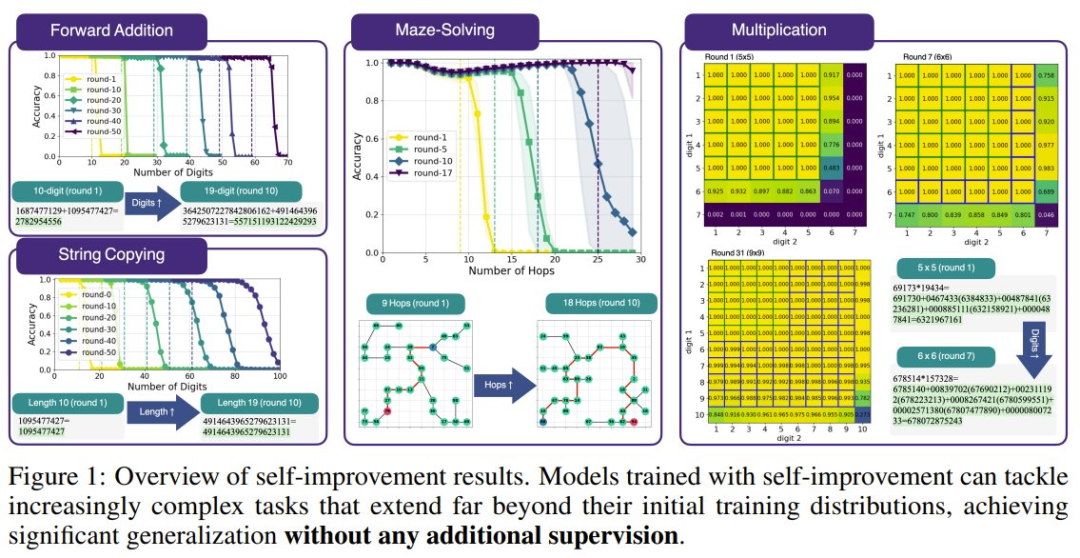
不僅如此，該團(tuán)隊(duì)還發(fā)現(xiàn)，自我改進(jìn)不僅限于長(zhǎng)度泛化，還可以實(shí)現(xiàn)從易到難的泛化，即在簡(jiǎn)單任務(wù)上訓(xùn)練的模型無(wú)需額外監(jiān)督即可成功學(xué)習(xí)更難的任務(wù)。值得注意的是，該方法并沒(méi)有引入新的自我改進(jìn)框架，而是展示了其在各種算法任務(wù)中的有效性。

此外，他們還研究了自我改進(jìn)的動(dòng)態(tài)，并得到了以下發(fā)現(xiàn)：

首先，控制從弱到強(qiáng)的歷程非常重要，因?yàn)闉榱吮苊鉃?zāi)難性失敗，模型需要結(jié)構(gòu)化的難度調(diào)度計(jì)劃。

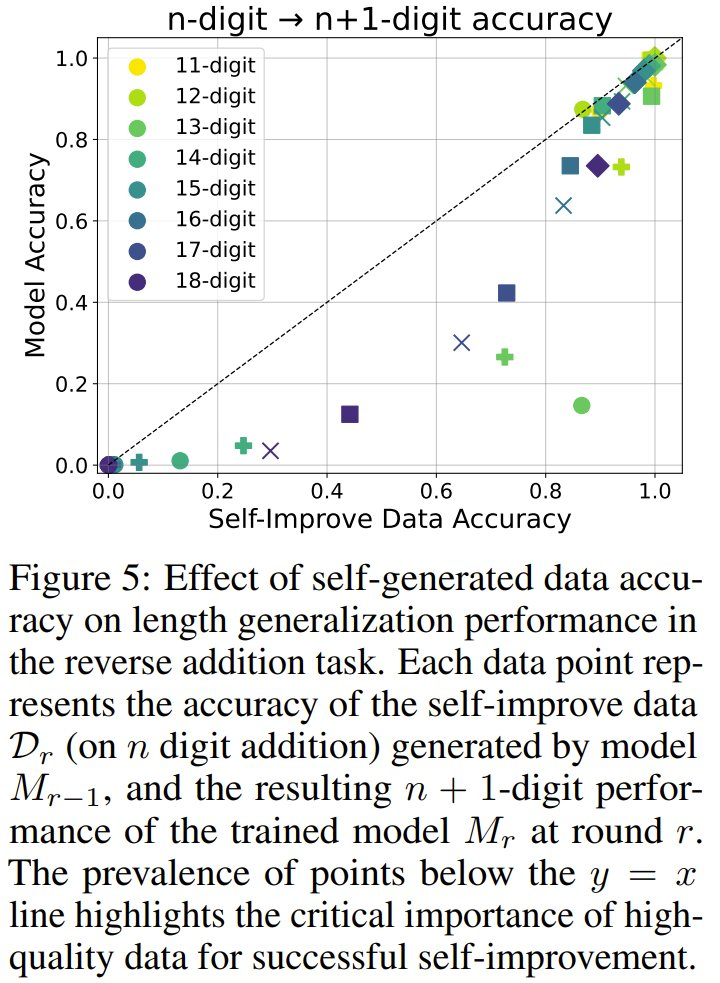
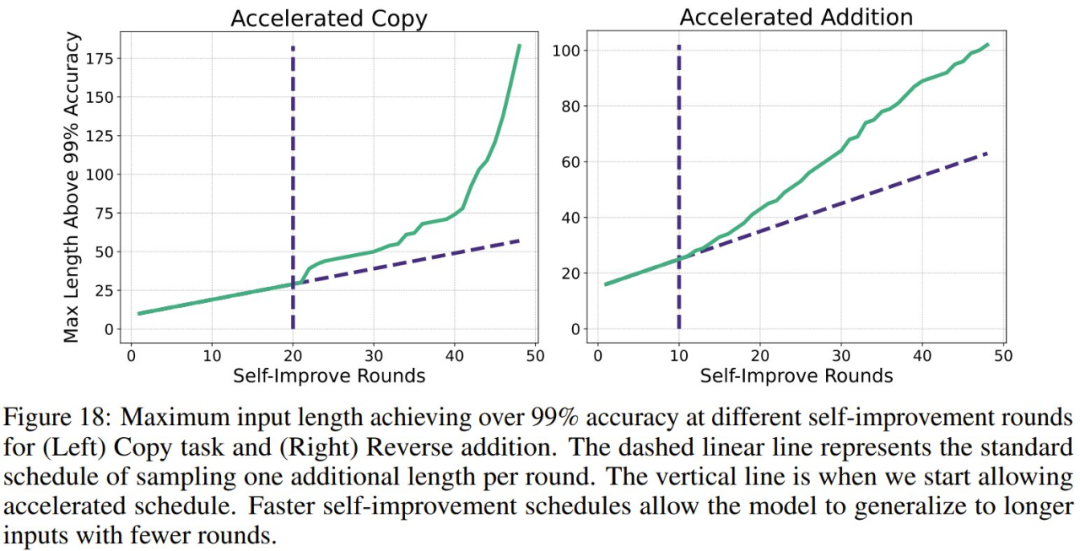
第二，自我改進(jìn)會(huì)隨著時(shí)間的推移而加速，因?yàn)楦щy的示例樣本會(huì)帶來(lái)越來(lái)越大的好處，在某些情況下會(huì)實(shí)現(xiàn)指數(shù)級(jí)的外推。

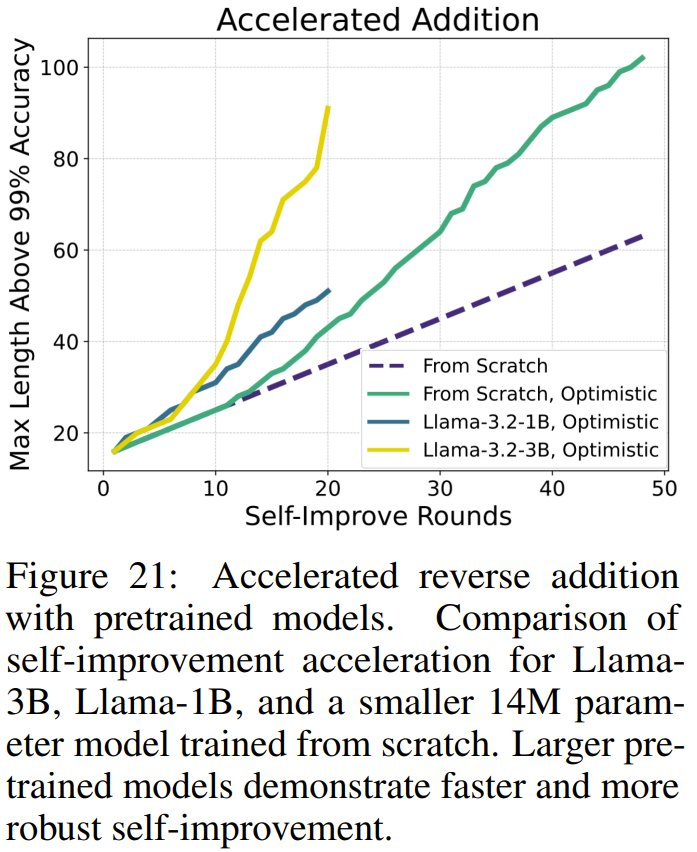
最后，如果從預(yù)訓(xùn)練模型開(kāi)始，可以顯著加快自我改進(jìn)速度，從而比使用從頭開(kāi)始訓(xùn)練的模型更快地實(shí)現(xiàn)泛化。

該團(tuán)隊(duì)總結(jié)說(shuō)：「我們的研究結(jié)果提供了證據(jù)，表明對(duì)于長(zhǎng)度泛化和從易到難泛化，學(xué)習(xí)自我改進(jìn)是一種通用且可擴(kuò)展的解決方案。」

那么，Transformer 大模型能做多位數(shù)乘法了嗎？

回到最開(kāi)始的問(wèn)題，如果使用自我改進(jìn)，基于 Transformer 的大模型能就能做多位數(shù)乘法了嗎？

先來(lái)看看實(shí)驗(yàn)結(jié)果，當(dāng)組合使用多數(shù)投票與長(zhǎng)度過(guò)濾時(shí)，31 輪提升后，實(shí)驗(yàn)?zāi)Ｐ湍茉?9 位數(shù)以?xún)?nèi)的乘法上達(dá)到近乎完美的表現(xiàn)。

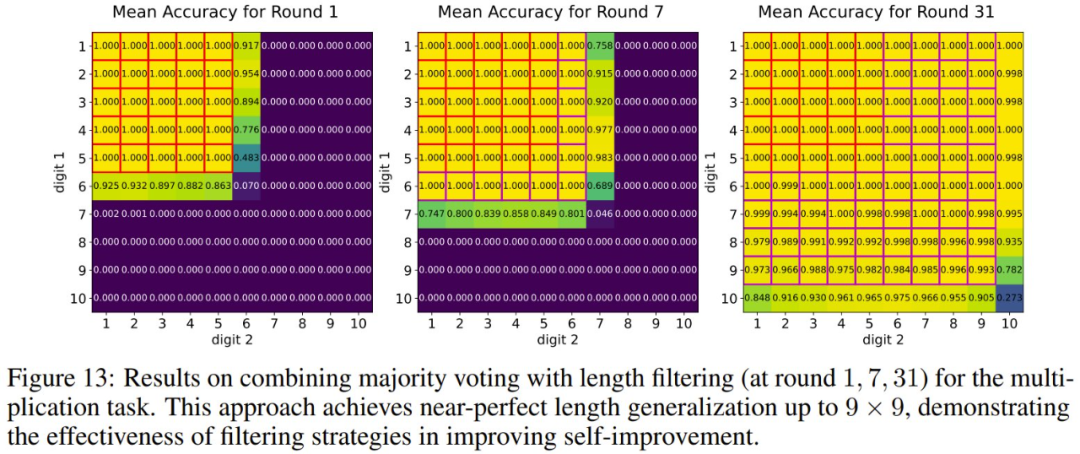
而如果使用該團(tuán)隊(duì)精心設(shè)計(jì)的一種自我改進(jìn)調(diào)度方案，提升速度還能大大提升：在 19 輪內(nèi)就能在 10 位數(shù)以?xún)?nèi)的乘法上達(dá)到近乎完美。

不過(guò)，或許是實(shí)驗(yàn)成本方面的考慮，該團(tuán)隊(duì)并未實(shí)驗(yàn)更多位數(shù)的乘法。但至少?gòu)内厔?shì)上看，這種自我提升策略確實(shí)是可行的。

那么，問(wèn)題來(lái)了：現(xiàn)在的大模型已經(jīng)開(kāi)始有能力使用工具了，對(duì)于這樣的算術(shù)運(yùn)算，為什么不直接讓大模型調(diào)用一個(gè)計(jì)算器應(yīng)用呢？

對(duì)此，Dimitris Papailiopoulos 給出的答復(fù)是可以研究 Transformer 可以如何學(xué)習(xí)算法以及如何讓 Transformer 在比其訓(xùn)練數(shù)據(jù)更困難的數(shù)據(jù)上取得更好的表現(xiàn)。

本文轉(zhuǎn)自機(jī)器之心  ，作者：機(jī)器之心

原文鏈接:??https://mp.weixin.qq.com/s/nFltEWUts-8IM1z5GawlYw??