前面我們介紹了用于時間序列概率預測的分位數(shù)回歸，今天繼續(xù)學習基于概率預測的時間序列概率預測方法--共形預測。

現(xiàn)實世界中的應用和規(guī)劃往往需要概率預測，而不是簡單的點估計值。概率預測也稱為預測區(qū)間或預測不確定性，能夠提供決策者對未來的不確定性狀況有更好的認知。傳統(tǒng)的機器學習模型如線性回歸、隨機森林或梯度提升機等，旨在產(chǎn)生單一的平均估計值，而無法直接給出可能結(jié)果的數(shù)值范圍。如何從點估計擴展到預測區(qū)間，正是現(xiàn)代時間序列建模技術所關注的重點。

在預測建模中，我們知道模型的目標是為條件均值給出無偏估計。估計值與實際樣本值之間的差距被稱為誤差，體現(xiàn)了模型的不確定性。那么，如何量化這種不確定性呢?由于誤差代表了估計值與實際值之間的偏差，因此我們可以通過分析誤差的分布來量化不確定性的程度。

共形預測(Conformal Prediction，CP)正是一種基于這一思路的預測方法。它利用歷史數(shù)據(jù)，根據(jù)新的預測樣本點在已知誤差分布中的位置，為這個新預測給出一個范圍估計，使其以期望的置信度(如95%)落入此范圍內(nèi)。值得注意的是，CP是一種與具體模型無關的元算法，可以應用于任何機器學習模型，從而將點估計擴展到概率預測區(qū)間。

概率預測的優(yōu)勢在于，它不僅給出預測的平均水平，還能提供相應的不確定性量化信息。這種額外的不確定性信息對風險管理、決策優(yōu)化等應用場景至關重要。比如在供應鏈、庫存管理等領域，通過概率預測可以權(quán)衡需求波動的風險，制定更加魯棒的規(guī)劃策略。

什么是共形預測

Conformal Prediction是一種非參數(shù)方法，用于生成具有概率保證的預測區(qū)域。它不依賴于特定的概率分布假設，而是通過計算數(shù)據(jù)點的“相似性”或“一致性”來產(chǎn)生預測。這種方法可以應用于各種類型的輸入數(shù)據(jù)（如連續(xù)變量、分類標簽、時間序列等）和輸出（如回歸、分類、排序等）。

技術分析

該項目實現(xiàn)了一套Python庫，包含多種算法，如Inference for Regression, Multi-class Classification等，以支持Conformal Prediction的應用。關鍵步驟包括：

• 訓練集準備：首先，對數(shù)據(jù)進行預處理，并將其分為訓練集和驗證集。
• 構(gòu)建基礎模型：利用訓練集訓練一個基礎預測模型（如線性回歸、決策樹或神經(jīng)網(wǎng)絡）。
• 計算非conformity分數(shù)：對于每個驗證集樣本，使用模型生成預測，并計算其與實際觀測值的非conformity分數(shù)。
• 確定閾值：通過將這些非conformity分數(shù)排序并應用α-level，確定劃分預測區(qū)間的閾值。
• 預測階段：對于新的未標記數(shù)據(jù)，根據(jù)該閾值生成預測區(qū)間。

這種框架允許用戶在保持預測性能的同時，為預測誤差提供嚴格的概率保證。

應用場景

• 金融風險評估：在信貸評分中，可以預測未來的違約概率，并給出置信區(qū)間，幫助金融機構(gòu)做出更穩(wěn)健的決策。
• 醫(yī)學診斷：在醫(yī)療預測中，可以估計治療效果的范圍，為醫(yī)生提供更全面的信息。
• 市場趨勢預測：在商業(yè)環(huán)境中，可以預測銷售量或股票價格，為策略制定者提供可靠參考。

特點

• 靈活性：適用于不同類型的預測問題和數(shù)據(jù)類型。
• 可解釋性：提供的預測區(qū)間有助于理解模型的不確定性。
• 無假設：不需要對數(shù)據(jù)的底層分布做假設，增強了泛化能力。
• 概率保證：可以量化錯誤率，提高預測的可靠性。

共形回歸(Conformal Regression)是一種獲得預測區(qū)間的有效方法，其構(gòu)造過程可以概括為以下幾個步驟:

1. 計算誤差分布 首先計算歷史數(shù)據(jù)中每個樣本點的預測誤差，即預測值與真實值之間的絕對差值。然后將這些誤差值從小到大排序。
2. 確定誤差臨界值 在排序后的誤差分布中，選取一個臨界值，使得小于等于該臨界值的誤差所占比例等于期望的置信度(如95%)。該臨界值被視為可接受的最大預測誤差。
3. 構(gòu)建預測區(qū)間 對于新的預測樣本點，其預測區(qū)間被設定為[預測值-誤差臨界值， 預測值+誤差臨界值]。根據(jù)誤差臨界值的選取，該預測區(qū)間能以期望的置信度(如95%)包含真實值。

共形回歸的優(yōu)勢在于，它是一種與具體模型無關的元算法，可以應用于任何機器學習回歸模型的結(jié)果之上，從點估計擴展到概率預測區(qū)間。其關鍵是利用歷史誤差分布來量化新預測的不確定性，為決策過程提供了更多不確定性信息。

需要指出的是，共形回歸所構(gòu)建的預測區(qū)間是保守的，其寬度會隨著置信度的提高而增加。在一些對過度保守不利的應用場景中，可以考慮引入其他校正方法來縮小區(qū)間寬度。另一方面，共形技術還可以推廣到分類、異常檢測等其他機器學習任務。

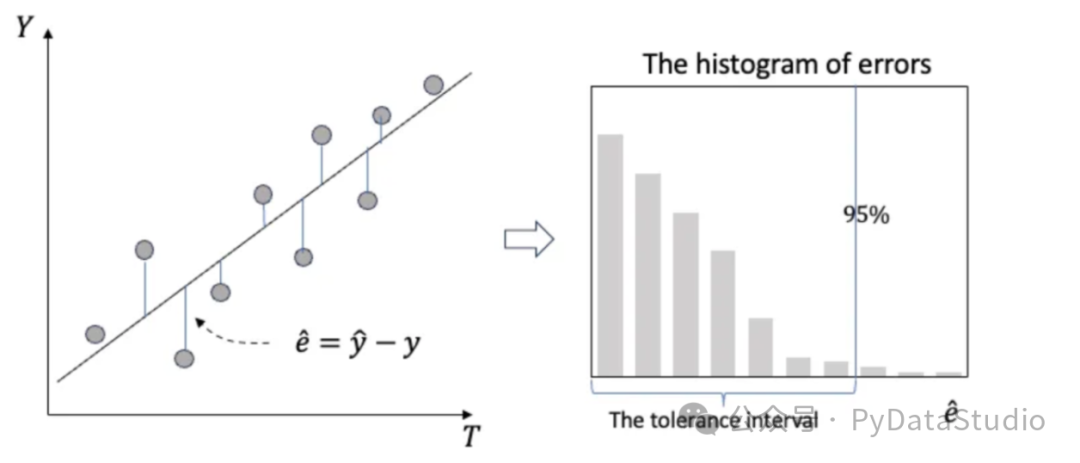
共形預測的構(gòu)造

這是在尋找預測區(qū)間的程序中使用的共形預測（CP）策略。請注意，它對模型規(guī)格和基礎數(shù)據(jù)分布不做任何假設。CP 與模型無關--適用于任何建模技術。共形預測技術由 Volodya Vovk、Alexander Gammerman 和 Craig Saunders（1999 年） 以及 Harris Papadopoulos、Kostas Proedrou、Volodya Vovk 和 Alex Gammerman（2002 年）提出。共形預測算法的工作原理如下：

• 將歷史時間序列數(shù)據(jù)分為訓練期、校準期和測試期。
• 在訓練數(shù)據(jù)上訓練模型。
• 使用訓練好的模型對校準數(shù)據(jù)進行預測。然后繪制預測誤差直方圖，并定義如圖 (A) 所示的容差水平。
• 將容差區(qū)間加減到任何未來點估算中，包括測試數(shù)據(jù)中的預測，以提供預測區(qū)間。

環(huán)境要求

在預測區(qū)間上，NeuralProphet 有三種選擇：(i) 分位數(shù)回歸 (QR)(ii) 共形預測 (CP)(iii) 共形分位數(shù)回歸 (CQR)。

你將按照標準安裝程序 pip install NeuralProphet 來安裝 NeuralProphet。

!pip install neuralprophet
!pip uninstall numpy
!pip install git+https://github.com/ourownstory/neural_prophet.git numpy==1.23.5

數(shù)據(jù)

這里我們將直接加載數(shù)據(jù)。這里的數(shù)據(jù)集可以直接在公眾號：數(shù)據(jù)STUDIO 里搜索 開源 23 個優(yōu)秀的機器學習數(shù)據(jù)集，這里有提供。

%matplotlib inline
from matplotlib import pyplot as plt
import pandas as pd
import numpy as np
import logging
import warnings
logging.getLogger('prophet').setLevel(logging.ERROR)
warnings.filterwarnings("ignore")
# 數(shù)據(jù)獲取：在公眾號：數(shù)據(jù)STUDIO 后臺回復 云朵君
data = pd.read_csv('/bike_sharing_daily.csv')
data.tail()

自行車租賃數(shù)據(jù)

這個數(shù)據(jù)集包含多變量數(shù)據(jù)，每天的租賃需求和其他天氣信息（如溫度和風速）。我們需要做最基本的數(shù)據(jù)準備來進行建模。NeuralProphet 要求列名為 ds 和 y。

# convert string to datetime64
data["ds"] = pd.to_datetime(data["dteday"])
df = data[['ds','cnt']]
df.columns = ['ds','y']

建模

使用一個簡單的 NeuralProphet 模型，包括趨勢和季節(jié)性模式，也可以加入其他成分，如 AR、假期和其他協(xié)變量。

from neuralprophet import NeuralProphet, set_log_level
cp_model = NeuralProphet(
    yearly_seasnotallow=True,
    weekly_seasnotallow=True,
    daily_seasnotallow=False,
)
cp_model.set_plotting_backend("plotly-static")

訓練、驗證和測試數(shù)據(jù)

共形預測或共形分位數(shù)回歸技術的一個重要的步驟是將訓練數(shù)據(jù)分為訓練數(shù)據(jù)和驗證數(shù)據(jù)，驗證數(shù)據(jù)將用于構(gòu)建容差統(tǒng)計。

df_train, df_test = cp_model.split_df(df, valid_p=0.2)
df_train, df_cal = cp_model.split_df(df_train, freq="D", valid_p=1.0 / 11)
[df_train.shape, df_test.shape, df_cal.shape]
# [(532, 2), (146, 2), (53, 2)]

我們用三種顏色繪制數(shù)據(jù)子集。

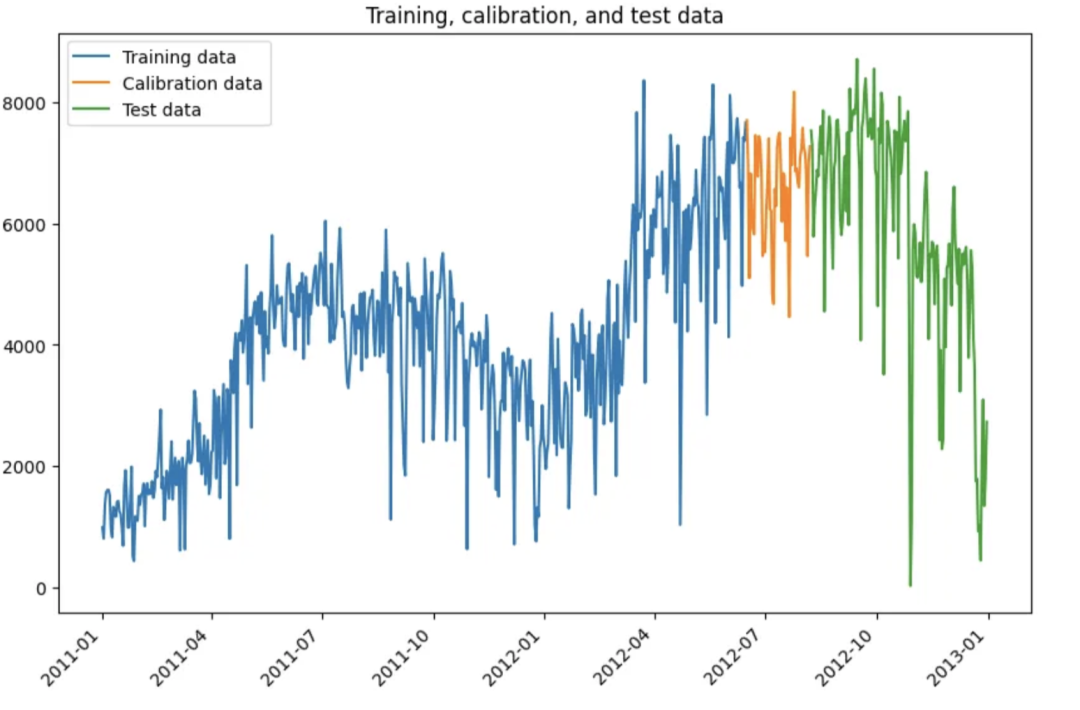圖片

我們使用驗證數(shù)據(jù)作為模型驗證集。

metrics = cp_model.fit(df_train, validation_df=df_cal, progress="bar")
metrics.tail()

圖片

然后，我們就可以進行預測并附加預測區(qū)間了。雖然 NeuralProphet 可以自動完成 CP，但我們還是要手動操作，以便向您展示操作步驟。

共形預測

我們計劃創(chuàng)建一個future數(shù)據(jù)集，該數(shù)據(jù)集將在df數(shù)據(jù)的最后日期之后延續(xù) 50 個周期。該數(shù)據(jù)集將包含模型對所有歷史數(shù)據(jù)的預測，或者如果我們設定n_historic_predictinotallow=40，則將僅包括 40 個歷史數(shù)據(jù)點及其預測結(jié)果。

NeuralProphet 的 CP 選項是 method=naive。我們將通過 .conformal_prediction()啟用保形預測。

future = cp_model.make_future_dataframe(df, periods=50, 
     n_historic_predictinotallow=True)

# Parameter for naive conformal prediction
method = "naive"
alpha = 0.05

# Enable conformal prediction on the pre-trained models
cp_forecast = cp_model.conformal_predict(
    # df_test, # You can also use df_test
    future,
    calibration_df=df_cal,
    alpha=alpha,
    method=method,
    show_all_PI=True,
)
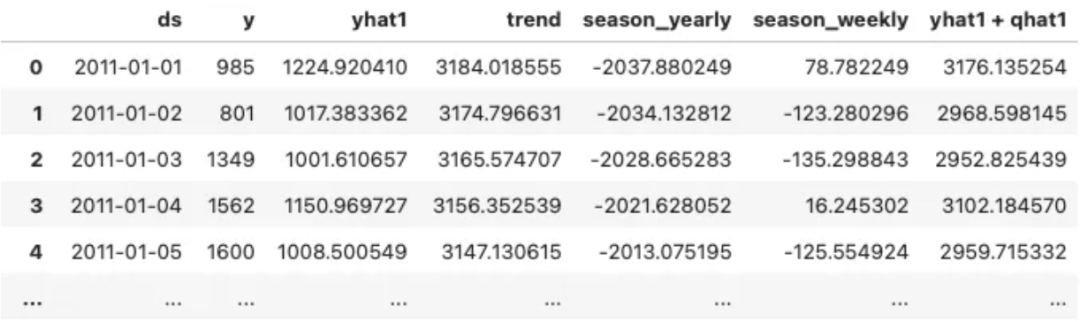
cp_forecast

輸出包含預測值 yhat1 和上限 yhat1 + qhat1。qhat1 是根據(jù)校準數(shù)據(jù)得出的容差范圍。

圖片

從 yhat1+qhat1中減去 yhat1即可得到 qhat1。這是一個 1951.214 的單一值。然后，我們可以通過從 yhat1減去 qhat1 得出下限。

cp_forecast['qhat1'] = cp_forecast['yhat1 + qhat1'] - cp_forecast['yhat1'] 
cp_forecast['yhat1 - qhat1'] = cp_forecast['yhat1'] - cp_forecast['qhat1']
cp_forecast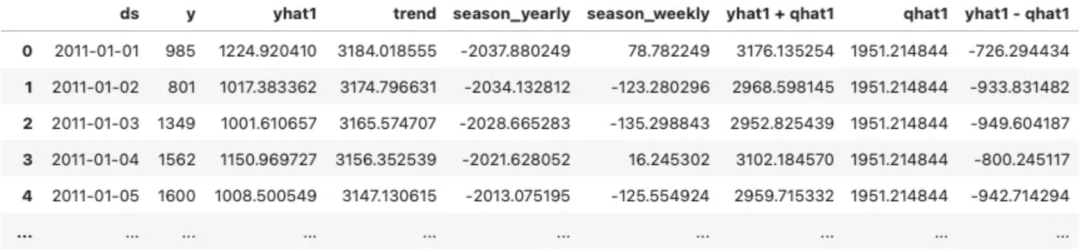

繪制預測值和預測區(qū)間圖。你會發(fā)現(xiàn)CP一直是一個固定值，在所有時段都是如此。它與預測值相加或相減得出上下限。

import matplotlib.pyplot as plt
plt.figure(figsize=(10,6))
#plot each series
plt.plot(df_train['ds'],df_train['y'], label='Training data')
plt.plot(df_cal['ds'],df_cal['y'], label='Calibration data')
plt.plot(df_test['ds'],df_test['y'], label='Test data')

plt.plot(cp_forecast['ds'],cp_forecast['yhat1'], label='Prediction')
plt.plot(cp_forecast['ds'],cp_forecast['yhat1 - qhat1'], label='Lower bound')
plt.plot(cp_forecast['ds'],cp_forecast['yhat1 + qhat1'], label='Upper bound')
plt.legend()
plt.title('Conformal prediction')
plt.xticks(rotatinotallow=45, ha='right')
# Draw a vertical dashed line
plt.axvline(x=df_test['ds'].tail(1), color='r', linestyle='--', linewidth=2) 
plt.show()

共形預測

公差區(qū)間是根據(jù)校準數(shù)據(jù)中的實際值得出的。

結(jié)論

本文介紹了共形預測技術，提供預測區(qū)間。共形預測的構(gòu)造不依賴于任何模型假設，可適用于任何模型。此外，我們展示了在NeuralProphet中構(gòu)建預測區(qū)間的代碼示例。一些人可能已經(jīng)注意到，預測區(qū)間在所有時間段都是相同長度的。在某些情況下，不同的預測間隔可能更有意義。