使用 CNN 進行時間序列預測！！
作者：程序員小寒
1D 卷積層（One-Dimensional Convolutional Layer）是卷積神經網絡（CNN）的基本組成部分，廣泛應用于處理一維序列數據，如時間序列分析、自然語言處理、語音識別等。
1D 卷積層（One-Dimensional Convolutional Layer）是卷積神經網絡（CNN）的基本組成部分，廣泛應用于處理一維序列數據，如時間序列分析、自然語言處理、語音識別等。
1D 卷積層是深度學習中用于處理序列數據的重要工具。它通過滑動窗口方式提取局部特征，并在多個通道間整合信息。1D 卷積為時間序列、語音信號和文本數據提供了高效的特征提取能力，同時通過參數共享和稀疏連接保持了模型的高效性和魯棒性。
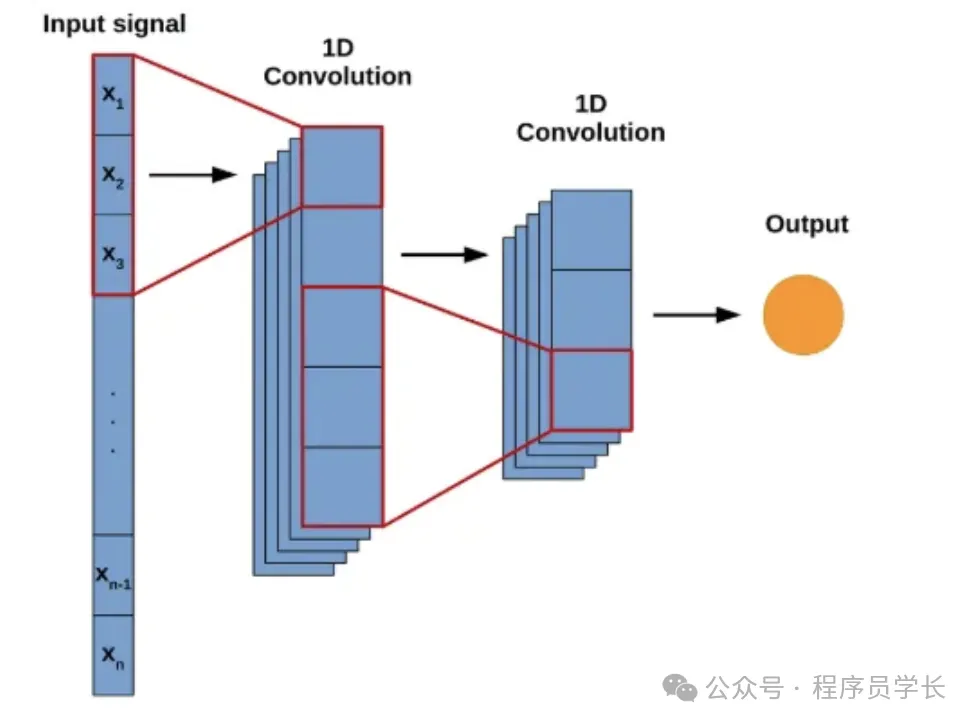
什么是1D卷積層
1D 卷積層通過滑動一個稱為卷積核（或濾波器）的窗口，在輸入序列上進行卷積操作，以提取局部特征。與2D卷積層主要用于圖像處理不同，1D 卷積層主要處理一維數據，如時間序列或文本序列。
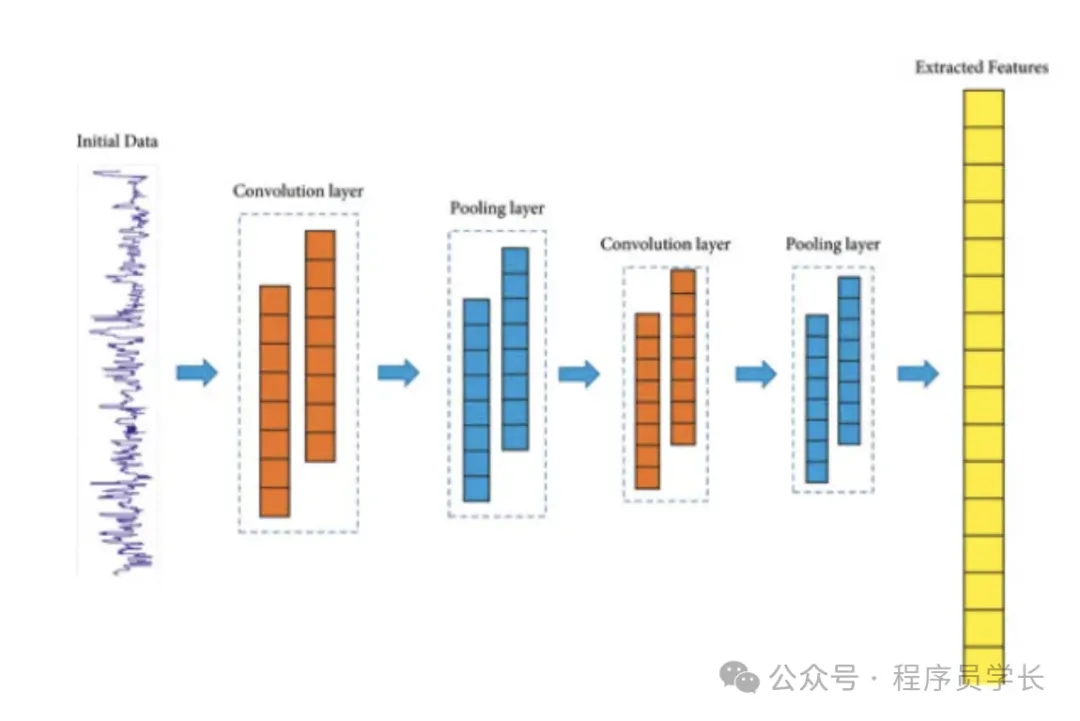
1D 卷積的基本原理
1D 卷積操作通過一個稱為卷積核（或濾波器）的固定大小的窗口，在輸入數據的一個維度上滑動，進行逐元素的點積運算，從而提取局部特征。
具體步驟如下：
- 輸入數據：假設輸入數據為一個長度為 L 的一維信號，可能具有多個通道（例如，多種傳感器數據）。
- 卷積核：設定一個長度為 K 的卷積核，通常會有多個卷積核以提取不同的特征。
- 滑動窗口：卷積核在輸入信號上以一定的步長（stride）滑動，每一步都與輸入信號的對應部分進行點積運算，并加上一個偏置項，生成一個輸出值。
- 輸出特征圖：滑動通過整個輸入信號后，生成一個新的特征序列，稱為特征圖（feature map）。
關鍵參數
- 卷積核大小（Kernel Size）
決定了每次卷積操作覆蓋的輸入范圍。
較大的卷積核可以捕捉更長范圍的依賴關系，但計算復雜度也相應增加。 - 步長（Stride）
卷積核每次滑動的步幅。較大的步長會減少輸出特征圖的長度，但可能導致信息丟失。 - 填充（Padding）
在輸入數據的邊緣添加額外的值（通常為零），以控制輸出特征圖的長度。 - 通道數（Channels）
每個卷積核可以有多個輸入通道，尤其在多通道輸入數據（如多傳感器數據）中常見。 - 激活函數（Activation Function）
通常在卷積操作后應用非線性激活函數，如 ReLU，以引入非線性能力。
1D 卷積層的應用
1D 卷積層廣泛應用于以下領域
- 時間序列分析：如股票價格預測、傳感器數據分析等，通過1D 卷積提取時間上的模式和趨勢。
- 自然語言處理（NLP）：用于文本分類、情感分析，通過提取詞語序列中的局部特征。
- 音頻信號處理：如語音識別、音樂分類，通過 1D 卷積提取音頻信號中的特征。
- 生物信息學：如基因序列分析，通過識別 DNA/RNA 序列中的模式。
優缺點
優點
- 參數共享：卷積核在整個輸入序列上共享參數，顯著減少了模型的參數數量，降低了過擬合的風險。
- 局部感受野：能夠有效捕捉輸入序列中的局部模式和短期依賴關系，對于處理具有局部相關性的序列數據非常有效。
- 計算效率高：由于參數較少，1D卷積層的計算復雜度相對較低，適合處理長序列數據。
- 平移不變性：卷積操作對輸入序列中的特定模式具有平移不變性，即模式在序列中的位置發生變化時，模型仍能有效識別。
- 靈活性強：可以通過堆疊多個卷積層或調整卷積核大小，捕捉不同尺度的特征。
缺點
- 長距離依賴捕捉能力有限
雖然堆疊多個卷積層可以擴展感受野，但在捕捉序列中長距離依賴關系時，1D卷積層可能不如循環神經網絡（RNN）或自注意力機制（如Transformer）有效。 - 特征提取的局限性
在某些復雜任務中，1D卷積層提取的特征可能不足以捕捉所有重要的信息，需要結合其他模型或技術進行增強。
案例分享
以下是分別使用 PyTorch 和 TensorFlow 實現 1D 卷積神經網絡來進行時間序列預測的示例代碼。
PyTorch 實現
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
# 生成示例時間序列數據
def generate_sine_wave(seq_length, num_samples):
x = np.linspace(0, 4 * np.pi, seq_length)
data = np.array([np.sin(x + np.random.uniform(0, 2 * np.pi)) for _ in range(num_samples)])
return data
# 數據準備
seq_length = 50 # 輸入序列長度
num_samples = 1000 # 樣本數
prediction_length = 1 # 預測的未來步數
data = generate_sine_wave(seq_length + prediction_length, num_samples)
# 劃分數據：輸入和目標
X = data[:, :-prediction_length] # 輸入序列
y = data[:, -prediction_length:] # 目標值
# 轉為 PyTorch 張量
X = torch.tensor(X, dtype=torch.float32).unsqueeze(1) # 添加通道維度 (batch, channel, seq_length)
y = torch.tensor(y, dtype=torch.float32)
# 劃分訓練和測試集
train_size = int(0.8 * len(X))
X_train, X_test = X[:train_size], X[train_size:]
y_train, y_test = y[:train_size], y[train_size:]
# 檢查數據形狀
print("訓練集輸入形狀:", X_train.shape) # (batch_size, channels, seq_length)
print("訓練集目標形狀:", y_train.shape) # (batch_size, prediction_length)
# 定義 1D 卷積預測模型
class Conv1DPredictor(nn.Module):
def __init__(self, input_channels, output_size, kernel_size=3):
super(Conv1DPredictor, self).__init__()
self.conv1 = nn.Conv1d(in_channels=input_channels, out_channels=16, kernel_size=kernel_size, padding=1)
self.conv2 = nn.Conv1d(in_channels=16, out_channels=32, kernel_size=kernel_size, padding=1)
self.fc = nn.Linear(32 * seq_length, output_size) # 全連接層，用于生成預測結果
def forward(self, x):
x = torch.relu(self.conv1(x)) # 第一層卷積 + 激活
x = torch.relu(self.conv2(x)) # 第二層卷積 + 激活
x = x.view(x.size(0), -1) # 展平
x = self.fc(x) # 全連接層輸出
return x
# 初始化模型
model = Conv1DPredictor(input_channels=1, output_size=prediction_length)
criterion = nn.MSELoss() # 損失函數
optimizer = optim.Adam(model.parameters(), lr=0.001) # 優化器
# 訓練模型
num_epochs = 50
train_losses = []
for epoch in range(num_epochs):
model.train()
optimizer.zero_grad()
output = model(X_train) # 前向傳播
loss = criterion(output, y_train) # 計算損失
loss.backward() # 反向傳播
optimizer.step() # 更新權重
train_losses.append(loss.item())
if (epoch + 1) % 10 == 0:
print(f"Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}")
# 測試模型
model.eval()
with torch.no_grad():
y_pred = model(X_test)
test_loss = criterion(y_pred, y_test)
print(f"測試集損失: {test_loss.item():.4f}")
# 可視化結果
plt.figure(figsize=(10, 5))
plt.plot(y_test.numpy()[:50], label="True Values")
plt.plot(y_pred.numpy()[:50], label="Predictions")
plt.legend()
plt.title("Time Series Prediction")
plt.show()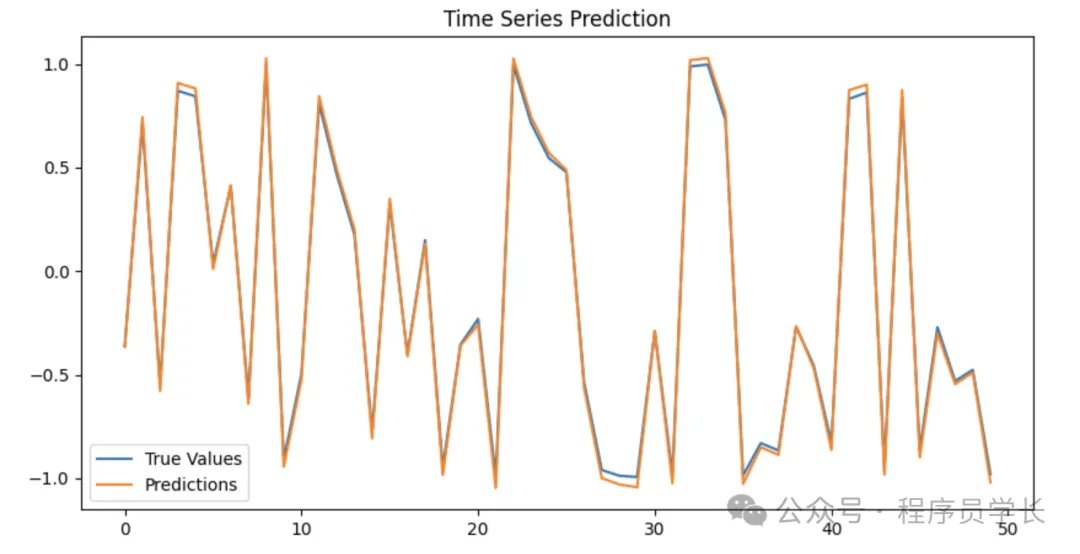
TensorFlow 實現
import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv1D, Dense, Flatten
from tensorflow.keras.optimizers import Adam
import matplotlib.pyplot as plt
# 生成示例時間序列數據
def generate_sine_wave(seq_length, num_samples):
x = np.linspace(0, 4 * np.pi, seq_length)
data = np.array([np.sin(x + np.random.uniform(0, 2 * np.pi)) for _ in range(num_samples)])
return data
# 數據準備
seq_length = 50 # 輸入序列長度
num_samples = 1000 # 樣本數
prediction_length = 1 # 預測未來步數
data = generate_sine_wave(seq_length + prediction_length, num_samples)
# 劃分數據：輸入和目標
X = data[:, :-prediction_length] # 輸入序列
y = data[:, -prediction_length:] # 目標值
# 劃分訓練集和測試集
train_size = int(0.8 * len(X))
X_train, X_test = X[:train_size], X[train_size:]
y_train, y_test = y[:train_size], y[train_size:]
# 擴展維度以適配 Conv1D 輸入格式
X_train = X_train[..., np.newaxis] # 轉換為 (batch_size, seq_length, channels)
X_test = X_test[..., np.newaxis]
# 檢查數據形狀
print("訓練集輸入形狀:", X_train.shape) # (batch_size, seq_length, channels)
print("訓練集目標形狀:", y_train.shape) # (batch_size, prediction_length)
# 構建 1D 卷積預測模型
model = Sequential([
Conv1D(filters=16, kernel_size=3, activatinotallow='relu', padding='same', input_shape=(seq_length, 1)),
Conv1D(filters=32, kernel_size=3, activatinotallow='relu', padding='same'),
Flatten(),
Dense(10, activatinotallow='relu'),
Dense(prediction_length) # 輸出層
])
# 編譯模型
model.compile(optimizer=Adam(learning_rate=0.001), loss='mse')
# 訓練模型
history = model.fit(X_train, y_train, epochs=50, batch_size=32, validation_split=0.2, verbose=1)
# 測試模型
test_loss = model.evaluate(X_test, y_test, verbose=0)
print(f"測試集損失: {test_loss:.4f}")
# 預測并可視化
y_pred = model.predict(X_test)
plt.figure(figsize=(10, 5))
plt.plot(y_test[:50], label="True Values")
plt.plot(y_pred[:50], label="Predictions")
plt.legend()
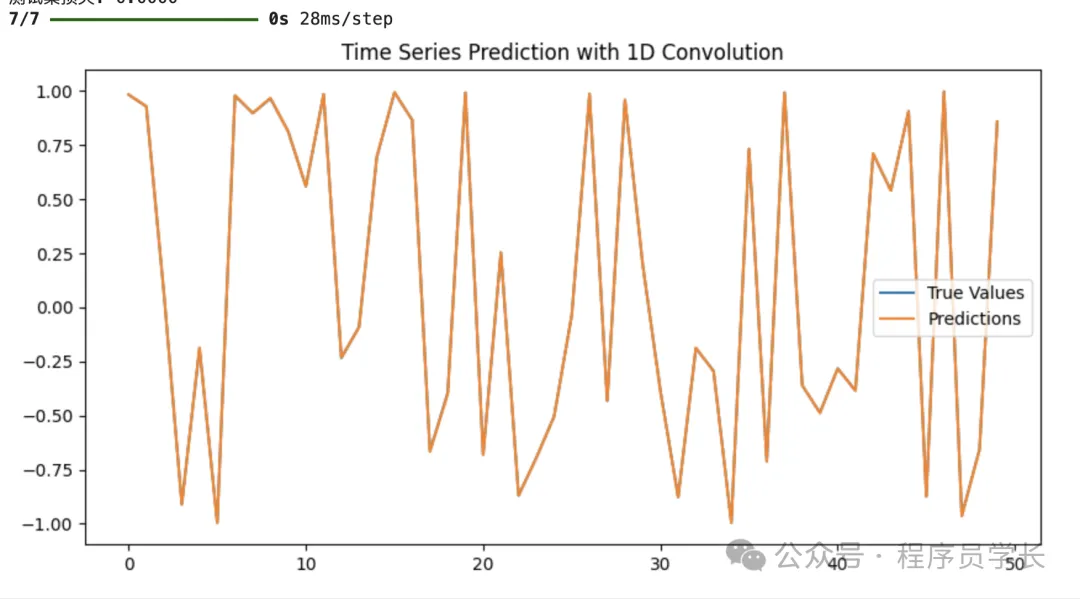
plt.title("Time Series Prediction with 1D Convolution")
plt.show()
責任編輯：華軒
來源：
程序員學長
